Spectrometer- Determination of Cauchy's constants

Aim:

To determine the Cauchy’s constant of the given prism.

  

Apparatus:

Spectrometer, prism, prism clamp, Magnifying glass, mercury vapor lamp, etc.

Theory:

Cauchy's equation is an empirical relationship between the refractive index and wavelength of light for a particular transparent material. It is named for the mathematician Augustin-Louis Cauchy, who defined it in 1836.


 
 The most general form of Cauchy's equation is

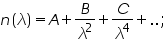   . . . . .. . . (1)

where n is the refractive index, λ is the wavelength, B, C, D, etc., are coefficients that can be determined for a material by fitting the equation to measured refractive indices at known wavelengths.

The refractive index n of the material of the prism for a wavelength λ is given by.

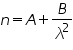                               . . . . ..  .. ..(2)

 Where A and B are called Cauchy’s constants for the prism.

If the refractive indices n1 and n2 for any two known wavelength λ1 and λ2 are determined by a spectrometer, the Cauchy’s constants A and B can be calculated from the above equation.

 

*The theory of light-matter interaction on which Cauchy based this equation was later found to be incorrect. In particular, the equation is only valid for regions of normal dispersion in the visible wavelength region. In the infrared, the equation becomes inaccurate, and it cannot represent regions of anomalous dispersion.

 

 

    Procedure

The angle of the prism A and the angle of minimum deviation D for different wave length are determined. From this the refractive index n for these colours are calculated. Taking the value of λ from the mathematical table, the Cauchy’s constants A and B are calculated for different pairs of spectral colours using the equation.

The Cauchy’s constants can also be determined graphically. A graph is drawn with n along the y-axis and 1/λ2 along x-axis with zero as the origin for both axes. The graph is a straight line. The Y intercept gives A and the slope gives B.

   

Table (1): To calculate A and B.

 

Table (2): To find A and B graphicaly.

Graph:

 Result:

Cauchy's constants
	A  =……………………………
	B  =…………………………… m2