Logistic map

#Logistic map function-Bifurcation Diagram

from pylab import *

def f(x):

    return c*x*(1-x)

c,cf=2,3.9  #2 is initail value of control para, 3.9 final vlaue

x=.2

xpt=[]

ypt=[]

while(c<=cf):

    for i in range(100):

        xpt.append(c)

        ypt.append(f(x))

        x=f(x)

    c=c+.01

plot(xpt,ypt,'.')

xlabel('Control parameter (c)')

ylabel('Population (x)')

show()

Output 

#Logistic map
from pylab import *
def f(c,x):
    return c*x*(1-x)
ci,cf,n,g,x0=2,3.9,100,100,.2
cs=(cf-ci)/1000.0
lx,lc=[],[]
for c in arange(ci,cf,cs):
    x=x0
    for i in range(g):
        x=f(c,x)
    p=0
    while p<n:
        x=f(c,x)
        lc.append(c)
        lx.append(x)
        p+=1
print lx
print lc
xlabel('Control parameter')
ylabel('Population')
plot(lc,lx,'.')
show()

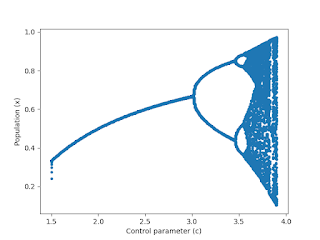
Output

  Theory :
#yn+1=c*yn(1-yn)
from pylab import*
c=float(input('input control parameter'))
i=1
y=.2
while i<73:
    y=c*y*(1-y)
    i=i+1
    print y

Values of yn for different  values of control parameter: