IDEAL SIMPLE HARMONIC OSCILLATOR-EULER METHOD

from pylab import *
n=100
x=zeros(n,dtype='float')
t=zeros(n,dtype='float')
v=zeros(n,dtype='float')
a=zeros(n,dtype='float')
x[0],v[0],w=0,2,1
dt=10*pi/(w*n)
a[0]=-w*w*x[0]
for i in range(1,n):
    a[i]=-w*w*x[i-1]
    v[i]=v[i-1]+a[i]*dt
    x[i]=x[i-1]+v[i]*dt
    t[i]=t[i-1]+dt
subplot(2,2,1)
title('t - x plot')
xlabel(' time (t)')
ylabel('displacement (x)')
plot(t,x)
subplot(2,2,2)
title('t- v plot')
xlabel('time (t)')
ylabel('velocity (v)')
plot(t,v)
subplot(2,2,3)
title('t- a plot')
xlabel('time (t)')
ylabel('acceleration (a)')
plot(t,a)
subplot(2,2,4)
axis('equal')
title('phase space plot')
xlabel('displacement (x)')
ylabel('velocity (v)')
plot(x,v)
show()

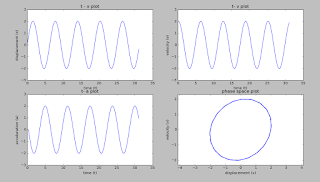
OUTPUT